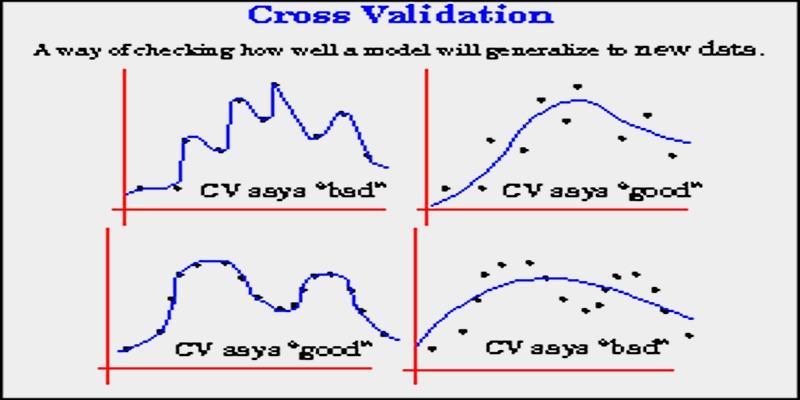
Cross-validation is another fundamental aspect of model testing in machine learning, and it is a factor that makes sure the algorithm can generalize to unseen data. But those mistakes are very easy to make; even the experienced practitioner can make such errors that skew the results. Appreciating and preventing most of the common traps during cross-validation can significantly enhance the reliability, accuracy, and practicality of the model.
Understanding the Role of Cross-Validation

In its simplest form, cross-validation is expected to address one question: How well can my model predict on unseen data? Through a systematic subdivision of the data set into multiple folds, training on a subset and validation on the rest, the practitioners are able to estimate the stability and predictive capability of a model.
Compared to other methods where the test set is split into one train or root (test) example, cross-validation averages performance using multiple splits, which provides a more extensive assessment. The process minimizes the chances of random variability in the conclusions, which makes it one of the most relied-upon processes in predictive modeling.
The idea, however, is rather simple and has to be refined when it comes to implementation. Data should be addressed with a high level of care, transformations to be applied in a proper sequence, as well as the natural structure of the dataset should be taken into account.
Pitfall One: Data Leakage Between Training and Validation Sets
The most threatening and misconstrued issue within cross-validation is, perhaps, the situation with data leakage, the unwanted flow of information belonging to the validation set into the training process. Leaked data gives a false impression of your model, as it might seem to do well on the testing data, but once in new data, it starts exhibiting a steep decline in accuracy.
Data leaks are commonly seen to take place during the preprocessing stages. As an illustration, assume a dataset that is already normalized or scaled, and then divided into training and validation. When this happens, both sets are affected by the same parameter, such as mean and standard deviation, which essentially leaves the model with some suggestions on the validation data.
To ensure that this is not the case, preprocessing should always be done after the data has been split. Every cross-validation fold must be treated as an independent training-validation pair with only scaling, encoding, or feature engineering fitted to the training sub-sample before acting on the validation sub-sample. This becomes accessible in libraries like scikit-learn, which facilitate pipelines enabling the automation of such transformations in a detached and reproducible way.
The Consequences of Data Leakage
The effects of data leakage are at times devastating but may be unnoticeable. A model that has been trained on leaked information will have jaw-droppingly high validation accuracy, which will provide an illusion of success. However, it does not work well in production due to the lack of the unholy advantage that existed when it was in training.
These deceptive results may be disastrous. Leakage could cause incorrect predictions of investments in financial forecasting, incorrect system optimizations in industrial analytics. The loss of months of hard work can be the result of even a minor data integrity violation.
The best method to mitigate line of defence leakage is to consider a train-only approach: regard validation information as highly confidential until the very last stage of analysis. Any preprocessing or transformation, or derivation of features should not exceed this boundary.
Pitfall Two: Ignoring Data Distribution and Temporal Order
The second most major error happened when the underlying structure or dependencies in the data were not taken into consideration. Conventional cross-validation is under the assumption that samples are independent and identically distributed. Regrettably, most data sets in the world do not live up to this assumption. With the presence of temporal or grouped dependence, random cross-validation will induce biases and provide a revised optimism of model performance.
An example is time series forecasting, where the values are always sequential; the value of today, this day, will be based on the value of yesterday. It is possible to randomly divide the data set so that the model can be trained on some of the future data points and tested on some of the past data points, and thus be given something akin to foresight, which would not occur in a real-life situation.
Likewise, in data grouped (user activity data or repeated observations of the same object), one fold may randomly include data of the same group, or of the same member, in both the training and validation sets, and evaluate biasedly.
It will depend on the type of data:
- Time Series: Cross-validation also makes sure that the first data always comes before the second, so that the information at hand in the future does not affect the past predictions.
- Group K-Fold: Cross-validation allows similar samples to be placed in one fold, and there should never be any overlap in terms of training and validation between groups.
Why Ignoring Structure Leads to Misleading Results?
Ignoring group or time dependencies leads to evaluation measures that are not tied to reality anymore. A model may seem to have an outstanding predictive power when, in reality, it has only been trained through memorizing patterns that cross both training and validation folds.
Suppose that there is a recommendation system in which data belonging to the same user occur both during training and testing. This may merely be a result of the fact that the model knows the preference of that user, and not its predictive powers on similar users.
Building Robust Evaluation Practices
The things to avoid are just half of the battle. Intense, repetitive assessment procedures are the means to consistency and equity in the course of experimentation. The following are the habits underlying a stronger cross-validation strategy:
- Choose to use some folds that are appropriate to trade off between the computation cost and statistical stability, usually between 5 and 10.
- Use stratified sampling to classify problems in order to keep all folds with equal class ratios.
- Select metrics of evaluation that show actual goals, because there are other considerations, such as false positives or false negatives, that are not necessarily reflected by accuracy alone.
- Record each process of preprocessing, feature selection, and validation strategy to ensure transparency and reproducibility.
These practices assist in the assurance that even the complicated models are readable, equitable, and reliable once put into application.
Conclusion
Cross-validation, when executed correctly, remains one of the most reliable tools for assessing model generalization. However, the presence of data leakage or ignorance of data structure can render even the most advanced algorithms ineffective. By understanding and addressing these two critical pitfalls—data leakage and improper handling of data dependencies—practitioners can ensure that their models perform as intended when encountering real-world data.